I’ve mentioned a couple of times before that contest math is forming an important part my personal goals for math learning. I previously posted the solution to a challenging contest math problem, which showed how to use some clever algebraic manipulations to significantly simplify a particular sum. In this post, I solve another problem from the same resource (The Art of Problem Solving, Volume 1, a.k.a. AoPSv1), this time involving classical Euclidean geometry in the plane.
I’ll start by stating the problem, and then will indicate a blind alley I went down when trying to solve it. I’ll then present my version of a correct solution. It’s really a beautiful problem, putting together a bunch of difference concepts from the standard geometry curriculum.
1 A geometry problem
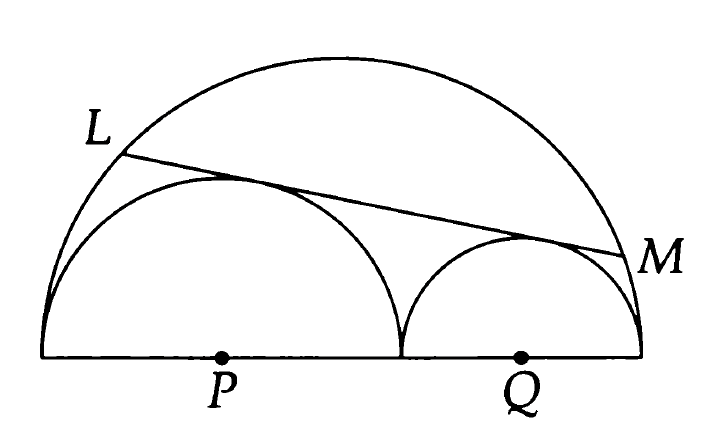
The statement of the problem appears as follows:
In Figure 1,1 the semicircles centered at \( \pts{P} \) and \( \pts{Q} \) are tangent to each other and to the large semicircle, and their radii are \( 6 \) and \( 4 \), respectively. Line \( \pts{LM} \) is tangent to semicircles \( \pts{P} \) and \( \pts{Q} \). Find \( \pts{LM} \).
It appears as problem 387 in The Art of Problem Solving, Volume 1 (p. 194), and is taken from the Mandelbrot Competition founded by AoPS authors Sandor Lehoczky and Richard Rusczyk with mathematician and math teacher Sam Vandervelde.
1.1 A blind alley
My first attempt at solving the problem ended in a blind alley. I include it here because seeing how even a fairly experienced math student (i.e., me) can go completely wrong can be quite instructive, as well as possibly serving as a morale boost if you even get stuck yourself (i.e., “It happens to everyone”).
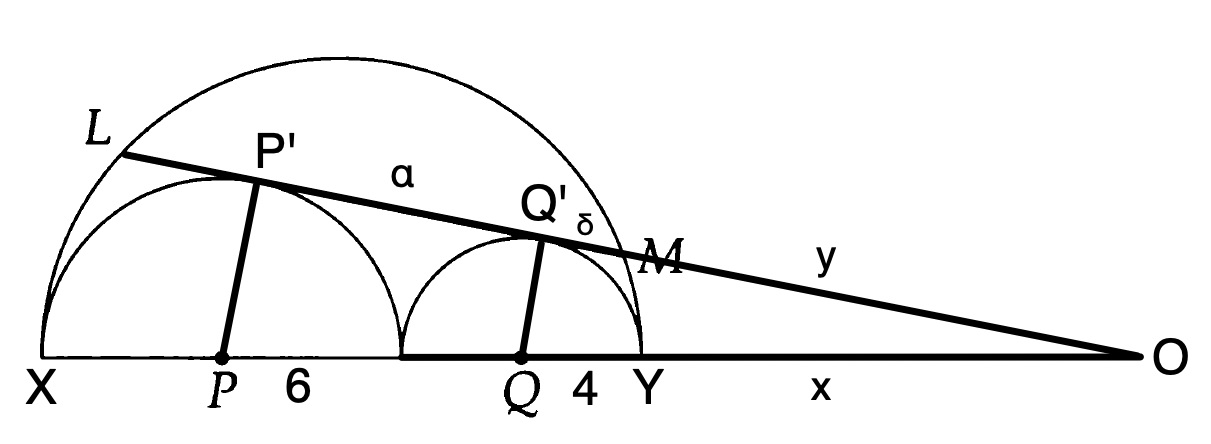
I’ll put what follows in a big block quote to separate the blind alley from the correct solution that follows it. (If you don’t care about the blind alley, you can skip directly to the solution in Section 1.2.)
This is a challenging problem. Let’s write down everything we know about it. Referring to Figure 2, we have
\[ \frac{6 + 2(4) + x}{6} = \frac{4 + x}{4} \]by similar triangles. (The origin of these terms is treated in more detail in Section 1.2.) Cross-multiplying gives
\[ 6(4 + x) = 4(6 + 2(4) + x) \]or
\begin{equation} \label{eq:prob_387_x} 24 + 6x = 56 + 4x \implies 2x = 32 \implies x = 16. \end{equation}
The Art of Problem Solving includes some nice theorems on the lengths of secants and tangents under the name “Power of a Point Formulas” (Chapter 17, p. 155). In particular, for two secants as shown below, we have the relation \( (AB)(AC) = (AD)(AE) \). See AoPSv1 Section 17.2 for a proof.
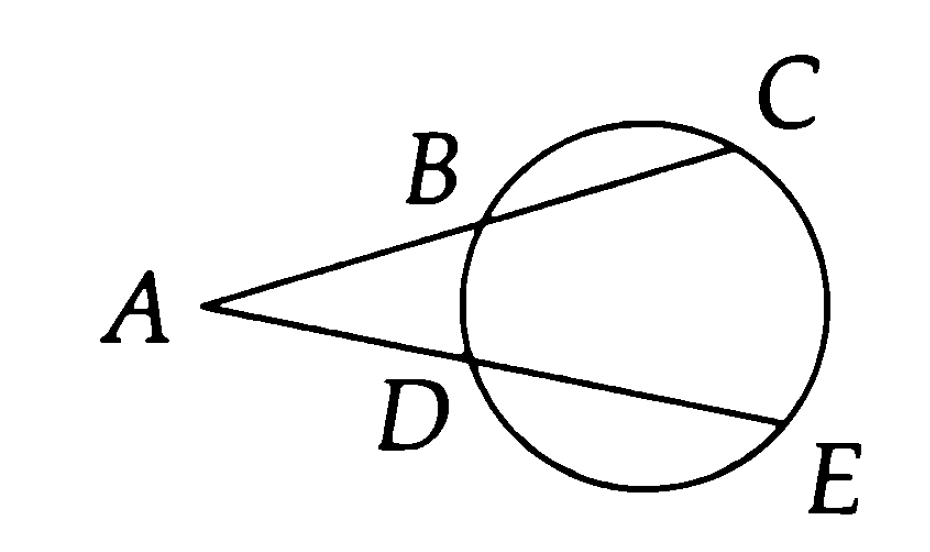
The secant–secant theorem (Box 1) gives
\[ (\pts{OY})(\pts{OX}) = (\pts{OM})(\pts{OL}) = (y)(y + \pts{LM}), \]where we have written \( y = \pts{OM} \) for convenience. With
\[ \pts{OX} = 2(6) + 2(4) + x = 12 + 8 + 16 = 36 \]and
\[ \pts{OY} = x = 16, \]we have
\[ (y)(y + \pts{LM}) = 16(36) = 576, \]so that
\begin{equation} \label{eq:prob_387_lm_om} \pts{LM} = \frac{576}{y} - y. \end{equation}The Pythagorean theorem gives
\begin{equation} \label{eq:y_plus_delta} (y + \delta)^2 = 4^2 + (x+4)^2 = 4^2 + 20^2 = 416 \implies y + \delta = 4\sqrt{26} \end{equation}and
\[ (y + \delta + \alpha)^2 = 6^2 + (x + 2(4) + 6)^2 = 6^2 + 30^2 = 936. \]Plugging in for \( y + \delta \) gives
\[ \alpha = \sqrt{936} - \sqrt{416} = 6\sqrt{26} - 4\sqrt{26} = 2\sqrt{26}. \]Similar triangles gives
\[ \frac{y + \delta + \alpha}{30} = \frac{y + \delta}{20} \]or
\[ 20(y + \delta) + 40\sqrt{26} = 30(y + \delta) \implies y + \delta = 4 \sqrt{26}, \]which we already knew from Eq. (3). Hmm.
1.2 A correct solution
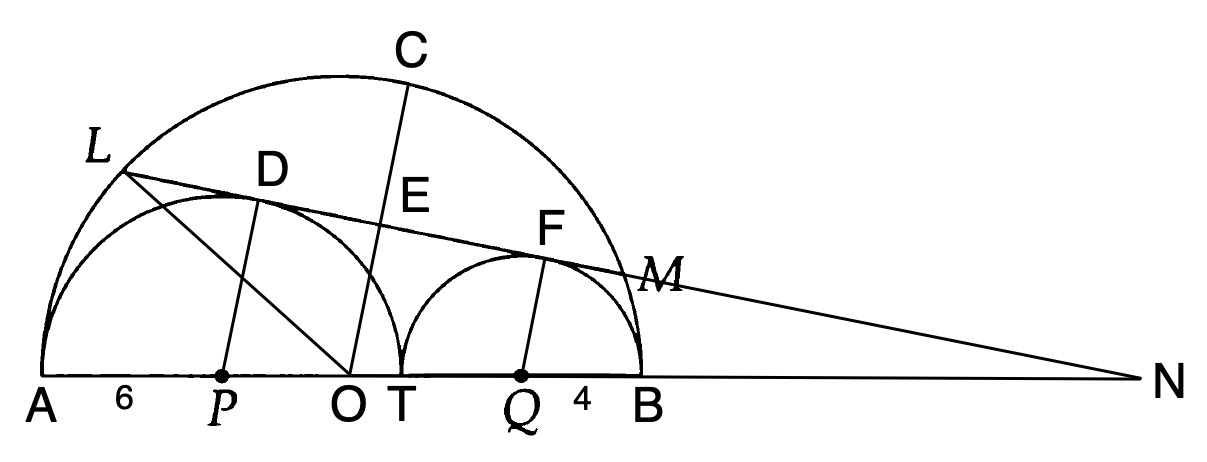
At this point, I thought, “This seems way too hard—there must be a trick.” Let’s try a different figure (Figure 3), which renames some points and adds \( \pts{LO} \) joining \( \pts{L} \) to \( \pts{O} \), the center of the largest circle, and draws \( \pts{OC} \) through \( \pts{O} \) parallel to \( \pts{PD} \) and \( \pts{QF} \). (See the next paragraph for how we know that these last two segments are parallel.) If we can get \( \pts{OE} \), we can find \( \pts{EL} \) by the Pythagorean theorem. Then, since a radius drawn perpendicular to a chord bisects it, we can double \( \pts{EL} \) to find \( \pts{LM} \).
We can get \( \pts{OE} \) using similar triangles. Because radii drawn to points of tangency are right angles, both \( \ang{NDP} \) and \( \ang{NFQ} \) are right. (This is how we know \( \pts{PD} \) and \( \pts{QF} \) are parallel: since corresponding angles are equal, the segments are parallel by Euclid’s Proposition 28.) Since \( \pts{OC} \) is parallel to \( \pts{PD} \) and \( \pts{QF} \) by construction, \( \ang{NEO} \) is also right by corresponding angles (which turns out is a postulate). Because of the shared \( \ang{N} \), the corresponding triangles are similar by Angle–Angle, so (using \( \sim \) to indicate similarity) we have \( \tri{NDP} \sim \tri{NEO} \sim \tri{NFQ} \).
One exercise I’ve decided to undertake as part of my math learning project is doing my best to find “mathematical bedrock”, that is, the foundational aspects of mathematics beyond which we can proceed no further. In the case of Euclidean geometry, this involves definitions, so-called “common notions”, and above all postulates that we assume to be true.
For example, what justifies the statement \( \pts{AB} = \pts{AT} + \pts{TB} \) in Eq. (4)? When I started this project, I wasn’t sure if that was a theorem that followed from more primitive notions or if it was something that we had to assume. The answer in this case is that we must assume it: the relation \( \pts{AB} = \pts{AT} + \pts{TB} \) follows from the segment addition postulate, which tells us that we are allowed to break segments into smaller pieces using points along the segment.
While these sorts of details are often left out of mathematical proofs, I’ve found it deeply satisfying to include them whenever possible. This practice makes crystal clear which elements of a proof are theorems (which we could in principle prove separately) and which are things we simply have to assume.
Let’s examine in detail how the similarity relationship \( \tri{NDP} \sim \tri{NFQ} \) allows us to determine the length of segment \( \pts{NB} \). Because we are given that the radius of circle \( \pts{P} \) is \( 6 \) and the radius of circle \( Q \) is \( 4 \), we can use the segment addition postulate (Box 2) to derive the relations
and hence
Since \( \pts{O} \) is the center of \( \pts{AB} \) by construction and the radius is half the diameter by definition, we have
Corresponding Parts of Similar Triangles are Similar (or CPSTS for short) is my own coinage, in analogy with Corresponding Parts of Congruent Triangles are Congruent (or CPCTC for short). In CPSTS, context determines the meaning of the second “Similar”: for angles, it means equal, while for sides it means proportional. Thus, using CPSTS, we can conclude that corresponding sides of similar triangles must have lengths in the same fixed ratio, while all their angles must be equal.
CPSTS (Box 3) then gives
Since \( \pts{PD} \) and \( \pts{QF} \) are radii of the respective circles, we have \( \pts{PD} = 6 \) and \( \pts{QF}= 4 \). Again applying the segment addition postulate, we get
and
Plugging the relevant values into Eq. (6) then gives
or
so that
Thus, \( \pts{NO} = \pts{NB} + \pts{OB} = 16 + 10 = 26 \).
Now we’ll apply the value \( \pts{NQ} = \pts{NB} + \pts{BQ} = 16 + 4 = 20 \). CPSTS with \( \tri{NEO} \sim \tri{NFQ} \) implies
or
so that
Reality check: from Figure 3, we see that \( \pts{OE} \) should be bigger than \( \pts{QF} = 4 \) and smaller than \( \pts{PD} = 6 \)—that is, we should have \( 4 < \pts{OE} < 6 \)—and indeed \( 26/5 = 5.2 \) satisfies this requirement.
Since \( \pts{OL} \) is a radius of the largest circle, it is equal to \( 10 \) by Eq. (5). Using the Pythagorean theorem then gives
or
Doubling this to get \( \pts{LM} \) finally gives
Somewhat amazingly, this is the right answer. My initial approach in Section 1.1 missed the construction of a radius from the center of the biggest circle parallel to the other two segments, as well as missing the right triangle from that center to \( \pts{L} \). Even after getting the right construction, it still took some thought to solve.
1.3 Review
Let’s make a list of the main ideas used in this problem:
Similar triangles (twice)
Tangent circles
The segment addition postulate
Radius equals half the diameter
A radius drawn to a point of tangency is perpendicular to the tangent line.
The Pythagorean theorem
A radius perpendicular to a chord bisects the chord.
It took all of those elements and more to derive the correct solution, which was far more involved than what we would typically find in a high-school geometry course. What a great problem!