This is a status update on my math learning project. I discuss some of the progress I’ve made, some lessons I’ve learned, and some adjustments I’m making.
Recall that I’m currently focusing on an introduction to rigorous mathematics (“intro to math”) with a focus on breadth and mathematical proof. I have multiple learning rounds planned—essentially, bundles of slots—and I’m thinking of this as the “zeroth” one, both because it’s foundational and because it includes a lot of material I already know (i.e., I’m borderline overqualified for it).
As discussed in Resources for Math Learning, I’m currently working on four slots, represented by four primary resources:
Pure Mathematics for Beginners by Steve Warner
How to Prove It by Daniel Velleman
The Art of Problem Solving, Volume 1 by Lehoczky and Rusczyk
Sage for Undergraduates by Gregory Bard
1 Three slots plus one
One nice feature of my current bundle of slots is that the slot on Sage is relatively easy. Moreover, once I finished a couple of chapters in Sage for Undergraduates, it wasn’t a blocker for any of the other slots.
After some experience managing multiple slots in parallel, I think this will be a general principle. Making progress on three primary slots is proving to be quite challenging on its own, so my current plan is to have each learning round consist of \( 3 + 1 \) slots, where the first three slots focus on core material and the final slot is more supplementary and not a blocker for future slots.1
Although my current \( +1 \) slot is Sage, going forward the best candidate for the \( +1 \) slot is contest math. Contest math problems are designed to apply subjects the contestant has already learned, so they should be great for reinforcing the core material. Contest math also doesn’t generally include any material that is a prerequisite for future rounds.
As it happens, though, this is not currently the case. In particular, The Art of Problem Solving includes a significant amount of material on number theory; since one of my planned slots for round 1 is exactly this subject, it makes sense to treat AoPS as a prerequisite for the next round. In addition, Pure Mathematics for Beginners and How to Prove It each include a chapter on this subject as well,2 so finishing all three should lead beautifully into a learning round containing a slot dedicated exclusively to elementary number theory.3
This has led to one of my major adjustments. Because AoPS consists of two volumes, and most of the number theory is in Volume 2, I realized I needed to put more time into finishing Volume 1 so that I can sync up all three primary slots before moving on to the next round. Accordingly, I have been working intensely on AoPS, Volume 1 ever since reaching a natural stopping point in Warner and Velleman (completing units in both books on mathematical logic). Once I’ve finished Volume 1 and I’m ready to move on to Volume 2, I plan to start advancing again in Velleman and Warner.
2 Current progress
So far I’ve made good progress in all four slots. As noted previously, I’ve already finished the core material in the \( +1 \) slot needed to use Sage for the other subjects. And in fact I’ve been using Sage for lots of things, including practicing the basics by using it to solve problems I can do by hand.
That brings us to the three primary slots. Regarding my main text for this round, I’ve finished just over half of Pure Mathematics for Beginners, enough to write a full post on it. (I’m planning to write separate posts on Velleman and AoPS once I’m done with them as well.) In the spirit of LATEX all the things!, so far I’ve produced 223 pages of notes and solutions, including answers to all of the Level 5 exercises.
I’ve also finished Velleman through Chapter 2, with 100 pages of notes and solutions. Both of the first two chapters of Velleman (plus an introduction) were jam-packed with great material, but unfortunately my progress seemed rather slow. To diagnose the problem, I tracked down a couple of university classes that use Velleman as a textbook, and discovered that I was doing 3–5 times as many problems as are assigned in a typical course. Although that means I was learning the material (mostly logic and set theory) quite thoroughly, that depth came at the expense of breadth and speed of progress. Keeping up forward momentum is important for morale, though, and I can always loop back later and do more problems. Thus, as another adjustment, I’m planning to do fewer problems per section once I start up again with Velleman after finishing Volume 1 of AoPS.
Speaking of which, I’m going gangbusters in The Art of Problem Solving, Volume 1: The Basics. I have now finished over 3/4 of the book, producing 222 pages of notes and solutions en route. AoPS has been simply a marvelous review of “high school” mathematics, including lots of results I either never knew or didn’t remember. To give you just a taste of it, I’ve included a couple of problems below, and I will include solutions in future posts. Good luck!
Two problems from AoPS
Exercise 7.2 in AoPS, Volume 1, Chapter 7 (“Special Factorizations and Clever Manipulations”): Find the sum
(This problem was mentioned previously in Personal Strategies for Math Learning.)
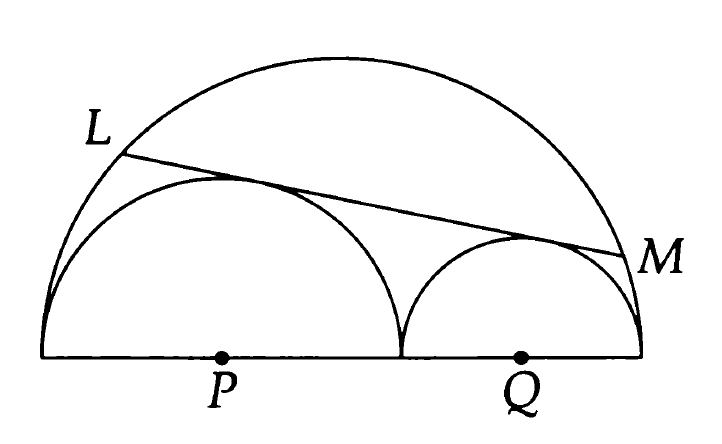
Problem 387 from Chapter 20 (“A Potpourri of Geometry”): In Figure 1, the semicircles centered at \( \mathit{P} \) and \( \mathit{Q} \) are tangent to each other and to the large semicircle, and their radii are \( 6 \) and \( 4 \), respectively. Line \( \mathit{LM} \) is tangent to semicircles \( \mathit{P} \) and \( \mathit{Q} \). Find \( \mathit{LM} \).