Time Dilation and the Star Trek Dream

I was recently at a party that involved a discussion of physics (no, I did not initiate this discussion), including various aspects of Einstein’s relativity. This led a friend of mine to lament that, due to the limit imposed by the speed of light, the dream of exploring the galaxy—à la Star Trek—could never be realized. As an ardent Trekkie, she said, this really bummed her out.

I replied by confirming that, as far as we can tell, the speed of light is a true upper limit, making a Star Trek–style “warp drive” a physical impossibility. But I also noted a loophole: due to an effect in special relativity known as time dilation, it’s actually possible to travel as far as you want on a spaceship in any given amount of ship time. In particular, the passage of time on the ship is slowed down relative to the observers you leave behind on Earth, and the faster you go relative to Earth, the slower time passes on the ship. This means you can always go as far as you want in a fixed amount of ship time as long as you pick a speed close enough to the speed of light.

images/figures/milky_way_galactic_center

The center of the Milky Way Galaxy.

She was pleased to hear of this loophole and later asked for more details. I responded with an example: if you wanted to go from the solar system to a point on the other side of the galactic center and back (Figure 1,¹ around \( 100,000 \) light-years round trip),² you could do it in only one year of ship time as long as you traveled at \( 99.999999995\% \) the speed of light. The big catch is that around \( 100,000 \) years would pass on Earth while you were gone, so you could expect that things would be very different by the time you got back. But as long as you brought everyone you want with you on the ship, you’d be good to go!

The way I got that \( 99.999999995\% \) number was by finding the speed required to travel a particular distance in a given amount of ship time. In the process of doing this calculation, I realized that the answer is especially elegant when expressed in terms of the light travel time to the desired destination. I have a fair amount of experience with this general subject (including teaching special relativity for four years when I was a graduate student at Caltech), but I didn’t recall ever having seen this exact calculation, so I thought I’d share it here.

1 Velocity as a function of ship time

Let’s make a precise statement of the problem: We want to find the speed required to travel a distance \( \Delta x \) in a fixed amount of ship time \( \Delta t_s \).³ For convenience, we’ll express the distance \( \Delta x \) in terms of the light travel time \( \Delta t_\ell \) to the destination. Since the speed of light \( c \) is a universal constant of nature, the two views are exactly equivalent, and we can always convert between the distance and time views by multiplying or dividing by \( c \). In particular, by definition of speed, the speed of light is just the distance traveled divided by the light travel time, so we can write

\begin{equation} \label{eq:speed_of_light} c = \frac{\Delta x}{\Delta t_\ell}. \end{equation}

Solving for \( \Delta t \) gives

\begin{equation} \label{eq:delta_t_ell} \Delta t_\ell = \frac{\Delta x}{c}. \end{equation}

By definition of light-year, \( c = 1~\text{light-year}/\text{year} \).⁴ Thus, in the example under consideration, \( \Delta x = 100,000~\text{light-years} \), and

\begin{align*} \Delta t_\ell & = \frac{\Delta x}{c} \\ & = \frac{100,000~\text{light-years}}{1~\text{light-year}/\text{year}} \\ & = 100,000~\text{years}. \end{align*}

For future reference, note that we can also solve Eq. (1) for \( \Delta x \):

\begin{equation} \label{eq:delta_x} \Delta x = c\Delta t_\ell. \end{equation}

Time dilation and the gamma factor

As noted above, the key physical effect in the problem is known as time dilation,⁵ and its mathematical expression in this case is

\begin{equation} \label{eq:time_dilation} \Delta t_E = \gamma \Delta t_s, \end{equation}

where \( \Delta t_E \) is the time on Earth, \( \Delta t_s \) is the time on the ship, and \( \gamma \) is the Lorentz gamma factor corresponding to the velocity⁶ \( v \) of the ship relative to Earth:

\begin{equation} \label{eq:lorentz_factor} \gamma = \frac{1}{\sqrt{1 - v^2/c^2}}. \end{equation}

(The derivation of time dilation is beyond the scope of this post, but it can be found in any good college-level textbook’s treatment of special relativity, such as Chapter 20 of Physics, Volume 1 by Resnick, Halliday, and Krane (as recommended in footnote 2 of my Feynman Lectures page).)

The Lorentz gamma factor as a function of velocity.

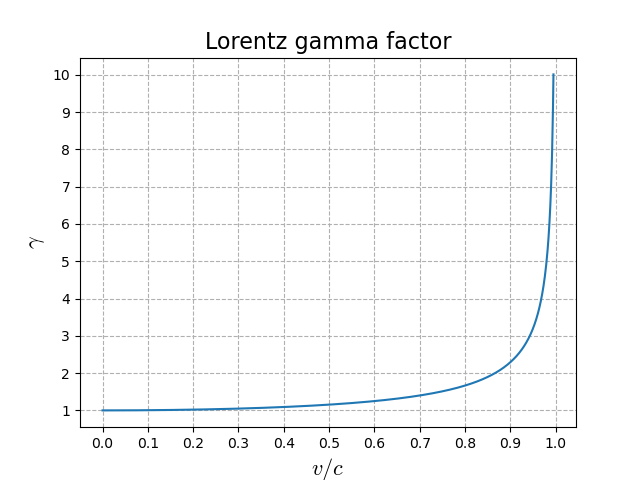
Note that when \( v = 0 \), Eq. (5) gives \( \gamma = 1 \), so that Eq. (4) becomes \( \Delta t_E = \Delta t_s \)—in other words, there is no time dilation effect. But as the velocity increases, the denominator of \( \gamma \)—namely, \( \sqrt{1 - v^2/c^2} \)—gets closer and closer to \( 0 \). As seen in Figure 2, this means that the value of \( \gamma \) rises rapidly as \( v \) gets close to \( c \) (or, equivalently, as \( v/c \) gets close to \( 1 \)).⁷

We can see why we can make the ship time as small as we want by solving Eq. (4) for \( \Delta t_s \):

\[ \Delta t_s = \frac{\Delta t_E}{\gamma}. \]

Because \( \gamma \) gets arbitrarily large as \( v \to c \), we can make the spaceship time \( \Delta t_s \) as small as we want by picking a velocity sufficiently close to the speed of light. Our task is to make this precise by deriving a formula telling us what this speed should be as a function of the desired ship time and the light travel time to the destination.

By definition of velocity, we can express \( v \) as the ratio of the distance traveled to the amount of Earth time \( \Delta t_E \):

\[ v = \frac{\Delta x}{\Delta t_E}. \]

Multiplying through by \( \Delta t_E \) lets us solve for \( \Delta x \):

\[ \Delta x = v\Delta t_E. \]

Plugging in the value of \( \Delta x \) from Eq. (3) then gives

\[ c\Delta t_\ell = v\Delta t_E, \]

so that

\[ \Delta t_E = \frac{c\Delta t_\ell}{v} = \frac{\Delta t_\ell}{v/c}. \]

It’s convenient to write this in terms of the commonly used auxiliary variable \( \beta = v/c \), which just expresses the velocity as a fraction of the speed of light:

\begin{equation} \label{eq:delta_t_E} \Delta t_E = \frac{\Delta t_\ell}{\beta}. \end{equation}

The Lorentz factor in Eq. (5) can also be written in terms of \( \beta \) as

\[ \gamma = \frac{1}{\sqrt{1 - \beta^2}}. \]

Squaring and inverting this gives the convenient relation

\begin{equation} \label{eq:gamma_squared_inverse} \frac{1}{\gamma^2} = 1 - \beta^2, \end{equation}

which we’ll put to good use in just a moment.

The key step

Now for the key step. Eq. (6) is simply a rearrangement of the definitions of distance and velocity, and hence is perfectly valid in classical Newtonian mechanics. But we can eliminate \( \Delta t_E \) in Eq. (6) using the value \( \gamma \Delta t_s \) from Eq. (4), which is a relativistic effect that has no analogue in nonrelativistic physics. The result is

\[ \gamma \Delta t_s = \frac{\Delta t_\ell}{\beta}, \]

\begin{equation} \label{eq:gamma_beta_inverse} \frac{1}{\gamma\beta} = \frac{\Delta t_s}{\Delta t_\ell}. \end{equation}

Let’s think about what the right-hand side of Eq. (8) represents: it’s the ratio of the ship time to the light travel time. The whole point of the Star Trek loophole is that we can make the ship time small compared to the light travel time, so let’s introduce the letter \( \varepsilon \) (typically used for small parameters) for this ratio:

\begin{equation} \label{eq:epsilon} \varepsilon = \frac{\Delta t_s}{\Delta t_\ell}. \end{equation}

Eq. (8) then becomes

\[ \frac{1}{\gamma\beta} = \varepsilon. \]

Squaring both sides and using Eq. (7) then gives

\[ \frac{1}{\gamma^2\beta^2} = \frac{1 - \beta^2}{\beta^2} = \varepsilon^2. \]

We can solve this for \( \beta^2 \) as follows:

\begin{align*} \frac{1 - \beta^2}{\beta^2} & = \varepsilon^2 \\ 1 - \beta^2 & = \varepsilon^2 \beta^2 \\ \varepsilon^2 \beta^2 + \beta^2 & = 1 \\ (1 + \varepsilon^2) \beta^2 & = 1 \\ \beta^2 & = \frac{1}{1 + \varepsilon^2}. \end{align*}

Taking square roots then gives us our key result:

\begin{equation} \label{eq:key_result} \beta = \frac{1}{\sqrt{1 + \varepsilon^2}}. \end{equation}

This formula lets us calculate the speed required (expressed as a fraction of the speed of light) to go a particular distance (as represented by a particular light travel time) in a particular amount of ship time.

A good approximation

Although we’re thinking of \( \varepsilon \) as a small parameter, so far the analysis has been exact within the context of special relativity, so Eq. (10) is correct even when \( \varepsilon \) isn’t small. We can derive a simpler equation for the main case we’re interested in—namely, when \( \Delta t_s \ll \Delta t_\ell \), corresponding to \( \varepsilon \ll 1 \)—using the power series expansion (written in terms of big \( O \) notation)

\[ (1 + x)^p = 1 + px + O(x^2), \]

which is valid for \( \left|px\right| \ll 1 \). Since \( 1/\sqrt{1 + \varepsilon^2} = (1 + \varepsilon^2)^{-1/2} \), Eq. (10) has this form with \( x = \varepsilon^2 \) and \( p = -1/2 \). In this case, \( \left|px\right| = \varepsilon^2/2 \ll 1 \) as required, so we can expand Eq. (10) as

\begin{align*} (1 + \varepsilon^2)^{-1/2} & = 1 + \left(-\frac{1}{2}\right)\varepsilon^2 + O(\varepsilon^4) \\ & = 1 - \frac{\epsilon^2}{2} + O(\varepsilon^4). \end{align*}

Ignoring higher-order terms then gives

\begin{equation} \label{eq:beta_approximate} \beta \approx 1 - \frac{\varepsilon^2}{2}. \end{equation}

For a ship time on the order of a year and a light travel time of around \( 100,000~\text{years} \), \( \varepsilon \sim 1/100,000 = 10^{-5} \implies \varepsilon^2 \sim 10^{-10} \). Since the error is of order \( \varepsilon^4 \sim 10^{-20} \), the higher-order terms are negligible compared to the leading term of \( 10^{-10} \), so the approximation in this case is very good indeed.

The final formula

Plugging in the definitions of \( \beta \) and \( \varepsilon \) lets us write Eq. (11) as

\begin{equation} \label{eq:key_result_v_t} \frac{v}{c} \approx 1 - \frac{1}{2}\,\left(\frac{\Delta t_s}{\Delta t_\ell}\right)^2. \end{equation}

Eq. (12) is the final and most convenient expression of the desired relation, giving us the speed \( v \) needed to go a light travel time of \( \Delta t_\ell \) in ship time \( \Delta t_s \), valid as long as \( \Delta t_s \ll \Delta t_\ell \).

Time to fly.

Referring to the example at the start of this post, for a ship time of \( \Delta t_s = 1\ \text{year} \) and a light travel of time of \( \Delta t_\ell = 100,000\ \text{years} \), we have \( \Delta t_s/\Delta t_\ell = 10^{-5} \), and thus Eq. (12) gives

\begin{align*} \frac{v}{c} & \approx 1 - \frac{(10^{-5})^2}{2} \\ & = 1 - 5\times10^{-11} \\ & = 0.99999999995. \end{align*}

Therefore, all we have to do to go to the other side of the galactic center and back in one year of ship time is travel at \( 99.999999995\% \) the speed of light (Figure 3).⁸

“And how can we arrange to go so fast?”, you might ask. Well, that’s just an engineering problem, of course!

1. Image retrieved from Wikimedia on 2024-01-12 and used under the terms of the Creative Commons Attribution 4.0 International license.

2. The solar system is approximately \( 25,000~\text{light-years} \) from the center of the Milky Way Galaxy, so going to a point the same distance on the opposite side would be around \( 25,000 \times 2 = 50,000 \) light-years, making for a \( 100,000 \)-light-year round trip. It’s worth noting that such a “there and back” calculation isn’t quite exact because the solar system orbits the center of the Milky Way Galaxy, so Earth’s position isn’t fixed relative to the galactic center, but the orbital period of around 225 million years is much longer than the \( 100,000 \)-year trip time, so to a good approximation we can ignore Earth’s change in position while the ship is en route.

3. The ship’s own time is sometimes called the “proper” time, but this terminology is a little confusing because it suggests that other times are somehow “improper”. In fact, the term comes from the French word propre, which means “own”.

4. Experienced students of relativity may recognize this as essentially equivalent to the convention of working in units where \( c = 1 \).

5. Specifically, time dilation caused by relative velocity, which is a special relativistic effect. Gravitational fields also cause time dilation, but this is a general relativistic effect and is not relevant to the problem at hand.

6. Technically, \( v \) is not the velocity but the speed (which is the magnitude of the velocity), but it is common in such contexts to use the terms interchangeably when no confusion is likely.

8. Image retrieved from stocksnap.io on 2024-01-12 and is in the public domain.